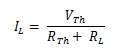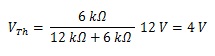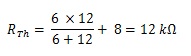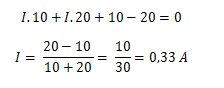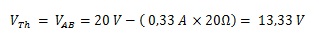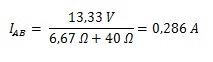Rangkaian Ekivalen Resistor & Contoh Soal Beserta Pembahasannya

Baik teman-teman semuanya, dalam postingan saya kali ini akan membahas tentang rangkaian ekivalen. Kebetulan hari ini mata kuliah yang diberikan dosen tentang rangkaian ekivalen resistor. Jadi untuk menambah pemahaman penulis, penulis mencari dari berbagai sumber untuk di satukan sebagai sebuah catatan dan untuk berbagi. Mari kita lihat di bawah ini. heheheheh.....

Rangkaian Ekivalen Resistor

(Rangkaian Pengganti Resistor)

Dua rangkaian disebut ekivalen jika antara dua terminal tertentu,  mereka mempunyai karakteristik i-v yang identik

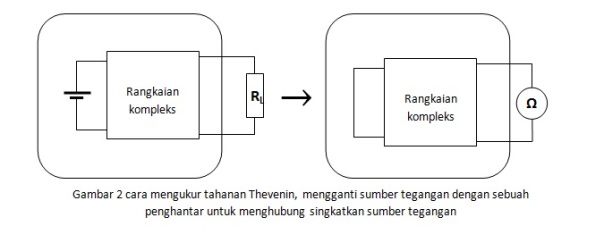
Teori Thevenin mengatakan bahwa sebuah rangkaian yang mengandung beberapa sumber tegangan dan hambatan dapat diganti dengan sebuah sumber tegangan yang dipasang seri dengan sebuah hambatan (resistor). Dengan kata lain rangkaian elektronika yang rumit dapat disederhanakan menjadi sebuah rangkaian hambatan linier yang terdiri dari 1 sumber arus dengan 1 resistor. Penyederhanaan rangkaian komplek menjadi sederhana dengan mengikuti teori Thevenin dapat dilihat seperti pada gambar berikut ini.

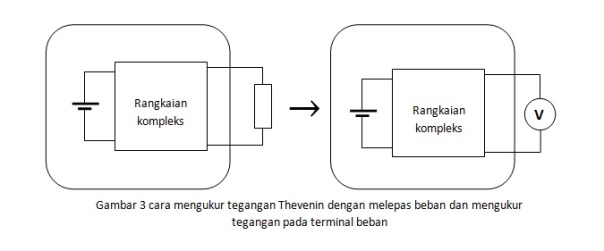
Pada gambar 1b terdapat sumber arus VTH yaitu tegangan Thevenin. Tegangan Thevenin adalah tegangan yang diukur atau dihitung pada terminal beban, ketika beban dilepas dari rangkaian. Karena diukur atau dihitung ketika beban dilepas, maka tegangan ini sering disebut tegangan rangkaian terbuka.

RTh disebut hambatan Thevenin. Hambatan Thevenin adalah hambatan yang diukur atau dihitung pada terminal beban ketika beban dilepas dari rangkaian dan sumber arus dibuat menjadi nol atau dihubung singkatkan. Untuk mengukur tahanan Thevenin kita harus mengurangi tegangan sumber arus hingga nol. Untuk sumber tegangan dapat di-nol-kan dengan menghubung-singkatkan terminal tegangan atau melepas sumber tegangan dan menggantikannya dengan sebuah penghantar. Gambar berikut ini menunjukan cara mengukur atau menghitung tegangan dan hambatan Thevenin.

Perhatikan gambar 2, terdapat sebuah black box yang terdiri dari sumber teganan DC dan rangkaian hambatan linier yang tidak diketahui bentuk rangkaiannya. Rangkaian hambatan linier adalah rangkaian yang hambatannya tidak berubah ketika tegangan dinaikkan atau diturunkan. Thevenin dapat membuktikan bahwa tidak peduli seperti apa bentuk rangkaian linier tersebut, tetapi semua rangkaian hambatan linier akan menghasilkan arus beban yang sama yang mengikuti persamaan :

Dimana : IL = arus beban ; VTh = tegangan Thevenin ; RTh = hambatan Thevenin dan RL = hambatan beban.

Contoh soal:

Berapakan nilai R_t atau tahanan ekivalen rangkaian campuran resistor dibawah ini?

Penyelesaian:
Pada gambar diatas tahanan-tahanan 56 Ω dan 33 Ω terhubung secara pararel, kemudian hubungan pararel ini dihubung seri dengan tahanan 47 Ω. 

Buat tahanan ekivalen R_t1 untuk hubungan pararel tahanan 56 Ω dan 33 Ω, dengan rumus pararel
1/R_t = 1/R₁ + 1/R₂ + 1/R₃ + · · · · · · + 1/R_n, maka
1/R_t1 = 1/56 + 1/33
1/R_t1 = 89/1848
89R_t1 = 1848
R_t1 = 1848/89
R_t1 = 20,8 Ω

Hubungan pararel tahanan 56 Ω dan 33 Ω dapat digantikan dengan tahanan ekivalen sebesar 20,8 Ω . Penyederhanaan ini menghasilkan dua buah tahanan yang terhubung secara seri, yaitu 20,8 Ω dan 47 Ω.

Nilai tahanan ekivalen rangkaian seri ini, sesuai rumus seri
R_t = R₁ + R₂ + R₃ + · · · · · · + R_n, maka
R_t = 20,8 + 47
R_t = 67,8 Ω

Sehingga diperoleh R_t atau sebuah tahanan ekivalen sebesar 67,8 Ω

Contoh soal 1 :

Hitung arus beban untuk besar hambatan beban RL = 2 kOhm, 4 kOhm dan 12 kOhm pada rangkaian berikut ini. Gunakan Teorema Thevenin !.

Jawab :

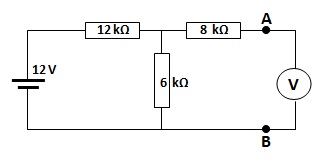
Langkah pertama, hitung besar tegangan Thevenin dengan cara melepas sumber tegangan dan menggantikannya dengan sebuah penghantar. Tegangan diukur atau dihitung pada terminal beban A-B seperti pada gambar berikut ini.

Besar tegangan Thevenin dapat dihitung :

Bila hambatan beban dilepas, maka tampak rangkaian menjadi rangkaian pembagi tegangan antara resistor 12 KΩ dengan resistor 6 kΩ sedangkan hambatan 8 kΩ tidak berpengaruh ke tegangan, hanya sebatas sebagai pembatas arus.

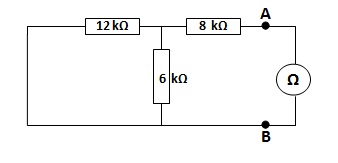
Langkah kedua adalah mengukur atau menghitung hambatan Thevenin dengan cara mengganti sumber arus dengan sebuah penghantar seperti pada gambar berikut ini.

Besar hambatan Thevenin dapat dihitung :

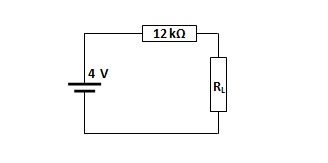
Langkah ketiga sederhanakan menjadi rangkaian Thevenin

Dengan RL bervariasi yaitu : 2 kOhm, 4 kOhm dan 12 kOhm. Maka besar arus yang melewati beban dapat dihitung :

Contoh soal 2: (sumber http://www.electronics-tutorials.ws)

Hitung arus yang mengalir melalui titik A-B (resistor 40 Ohm), gunakan teori Thevenin!

Jawab :

Pertama-tama hitung hambatan Thevenin pada titik AB seperti pada gambar berikut ini.

Besar hambatan A-B adalah :

Langkah kedua , hitung tegangan Thevenin seperti pada gambar berikut ini.

Gunakan hukum Kirchoff untuk menghitung tegangan pada titik AB.

Maka tegangan pada titik AB :

Langkah ketiga sederhanakan menjadi rangkaian Thevenin seperti pada gambar berikut ini.

Maka arus yang mengalir melalui titik AB adalah :

CONTOH PERMASALAH TENTANG TEORI RANGKAIAN THEVENIN

Pada gambar berikut ini menunjukkan sebuah rangkaian jembatan Wheatstone. Tentukan arus yang akan mengalir dengan beban 100Ω yang terhubung pada terminal A dan B.

Rangkaian Soal

CARA PENYELESAIAN CONTOH PERMASALAHAN DIATAS

Pertama , perlu kita tentukan persamaan / kesetaraan rangkaian Thevenin, Untuk menentukan nilai VOC kita bisa mengatur / merakit sebuah rangkaian jembatan sebagai pembagi tegangan.

Tegangan pada R2 dan R4 dapat dihitung dengan cara sebagai berikut:

V = 10 x (R2 / (R1 + R2))

V = 10 x (600 / (500 +600))

V = 10 x 0,5454

V = 5,454V

Maka didapatkan tegangan di A, relatif terhadap Y, yaitu 5,454V.

Untuk R4 :

V = 10 x (R4 / (R3 + R4)

V = 10 x (400 / (500 + 400))

V = 10 x 0,4444

V = 4,444V.

Maka didapatkan tegangan di B, relatif terhadap Y, yaitu 4,444V.

Tegangan VAB akan menjadi perbedaan antara VAY dan VBY, maka tegangan output rangkaian terbuka (VAB) akan menjadi:

VAB = VAY – VBY

VAB = 5,454 – 4,444

VAB = 1,01V

Selanjutnya kita perlu menemukan resistansi persamaan Thevenin. Untuk melakukan hal ini, kita dapat melakukan redraw rangkaian, seperti yang ditunjukkan pada skema berikut:

Rangkaian Setara / Persamaan

Nilai tahanan / hambatan setara nya adalah:

R = ((R1 x R2) / (R1 + R2)) + ((R3 x R4) / (R3 + R4))

R = ((500 x 600) / (500 + 600)) + ((500 x 400) / (500 + 400))

Demikian:

R = (300000/1100) + (200000/900)

R = 272 + 222,2

R = 494,9V

Rangkaian Thevenin ekuivalen ditunjukkan seperti gambar berikut:

Rangkaian Setara Persamaan 2

Untuk menentukan arus dalam beban 100Ω yang terhubung antara titik A dan B, kita dapat menggunakan rangkaian setara Thevenin dengan hanya menambahkan resistor ukuran 100Ω pada rangkaian dan menggunakan hukum Ohm. Seperti yang ditunjukkan gambar ini:

Rangkaian Setara Persamaan 3

Arus yang mengalir pada gambar diatas adalah:

I = ((V / (R + 100)) + ((10 / (494,9 + 100))

I = 10 / 594,9

I = 0,0168A

I = 16,8mA

CONTOH SOAL 

Hitung hambatan ekuivalen dari jaringan gambar dibawah dan carilah arus dalam setiap resistor . Sumber tegangan mempunyai hambatan dalam yang dapat diabaikan.

 

PENYELESAIAN

Gambar b dan c memperlihatkan tahapan berurutan dalam mereduksi jaringan itu menjadi sebuah hambatan ekuivalen tunggal. Dari persamaan pada resistor 6 ohm dan 3 ohm yang parallel dalam gambar a adalah equivalen dengan resistor 2 ohm tunggal dalam gambar b :

Dari persamaan gabungan seri dari resistor 2 ohm dan resistor 4 ohm adalah equivalen dengan 6 ohm tunggal dalam gambar c.

Untuk mencari arus dalam setiap resistor dari jaringan semula , kita membalik langkah-langkah yang kita gunakan ketika kita mereduksi jaringan itu. Dalam rangkaian yang diperlihatkan dalam gambar d ( yang identik dengan gambar c ) , arus itu adalah I = V/R = 18/6 = 3 A. Maka arus dalam resistor 4 ohm dan 2 ohm dalam gambar e ( yang identik dengan gambar b ) adalah juga 3 A. Selisih potensial V_ab yang melalui resistor 2 ohm adalah V_ab = IR = 3 . 2 = 6 V. Selisih potensial ini harus juga 6 V dalam gambar f ( yang identik dengan gambar a ). Dengan menggunakan I = V_ab/R, arus dalam resistor 6 ohm dan 3 ohm dalam gambar f berturut-turut adalah 6/6 = 1 A dan 6 /3 = 2 A.

Perhatikan bahwa untuk kedua resistor parallel antara titik c dan titik b dalam gambar f ada arus yang melalui resistor 3 ohm yang besarnya dua kali arus yang melalui resistor 6 ohm; lebih banyak arus yang melalui lintasan yang hambatan nya kecil. Perhatikan juga bahwa arus total yang melalui resistor-resistor ini adalah 3 A, sama seperti arus yang melalui kedua resistor tersebut 4 ohm diantara titim a dan c.

 

CONTOH SOAL – 2

Gabungan seri dibanding dengan gabungan parallel.

Dua bola lampu identik harus dihubungkan ke sebuah sumber dengan E = 8 V dan hambatan dalam yang dapat diabaikan . Setiap bola lampu mempunyai hambatan R = 2 ohm. Cari arus yang melalui setiap bola lampu , selisih potensial yang melalui setiap bola lampu, dan daya yang diantar kesetiap bola lampu dank e seluruh jaringan itu jika bola-bola iru disambungkan (a) seri dan (b) parallel (c) misalkan satu dari bola lampu itu terbakar , yakni filament lampu itu rusak dan arus tidak dapat lagi mengalir melalui serabut itu. Apa yang terjadi dengan bola lainnya dalam kasus seri dan kasus parallel ?

PENYELESAIAN

a) Dari persamaan resistor hambatan seri ekuivalen dari kedua lampu itu antara titim a dan titik c dalam gambar (a) adalah jumlah hambatan individunya, atau

R_ek = R + R = 4 ohm

Arus yang melalui masing masing bola lampu yang seri :

I = V_ac/ R_ek = 8/4 = 2 A

Karena bola bola lampu itu mempunyai hambatan yang sama , maka selisih potensial itu sama melalui setiap bola :

V_ab = V_bc = IR = 2 . 2 = 4 V

Nilai ini adalah setengah dari tegangan terminal 8 V dari sumber itu. Kita dapat mencari daya yang diantar ke setiap bola lampu dengan menggunakan salah satu rumus yaitu :

P = I² . R = 2² . 2 = 8 W atau

P = V²/R = 4²/2 = 8 W

Dimana V = 4 V adalah selisih potensial yang melalui sebuah bola lampu tunggal.

Daya total yang diantar kedua bola itu adalah P_total = 2P = 16 W. Secara alternative kita dapat mencari daya total itu dengan menggunakan hambatan ekuivalen R_ek = 4 ohm, yang melaluinya, arus adalah I = 2 A dan selisih potensial yang melewatinya adalah V_ac = 8 V:

P_total = I² . R_ek = 2² . 4 = 16 W atau

P_total = V_ac² /R_ek = 8² / 4 = 16 W

Kita menekankan bahwa arus I yang melalui kedua lampu itu sama besarnya. Bola-bola itu identik , sehingga daya P yang sama dihantar ke kedua bola itu, dan kedua bola tersebut akan menyala sama terangnya.

b) Jika bola bola itu parallel, seperti pada gambar (b) selisih potensial V_de yang melalui setiap bola adalah sama dan sama dengan 8 V, yakni tegangan terminal sumber itu. Maka arus yang melalui setiap bola lampu adalah

I = V_de /R = 8/2 = 4 A

Dan daya yang dihantar ke setiap bola lampu adalah

P = I² . R = 4² . 2 = 32 W atau

P = V² /R = 8² / 2 = 32 W

Kedua selisih potensial yang melalui setiap bola dan arus yang melewati setiap bola besarnya dua kali dari arus dalam kasus seri . Maka daya yang dihantar ke setiap bola adalah empat kali lebih besar , dan setiap bola menyala lebih terang dari pada dalam kasus seri. Jika tujuannya untuk menghasilkan jumlah cahaya maksimum dari setiap bola , maka susunan parallel lebih unggul daripada susunan seri.

Daya total yang dihantar ke jaringan parallel itu adalah P_total = 2P = 64 W, empat kali lebih besar dari pada pada kasus seri. Daya yang ditambah dibandingan dengan kasus seri tidak didapatkan “Cuma-Cuma” ; energy ditarik dari sumber empat kali lebuh cepat dalam kasus parallel daipada dalam kasus seri. Jika sumber itu sebuah aki , maka akan dihabiskan dalam waktu empat kali lebih cepat .

Kita juga dapat mencari daya total dengan menggunakan hambatan equivalen R_ek, yaitu :

Arus total yang melalui hambatan ekuivalen itu adalah I_total= 2 I = 2 . 4 = 8 A dan selisih potensial yang melalui hambatan ekuivalen itu adalah 8 V.

P_total = I² . R_ek = 8² . 1 = 64 W atau

P_total = V² /R_ek = 8² / 1 = 64 W

Selisih potensial yang melalui hambatan ekuivalen itu adalah sama untuk kedia kasus seri dan kasus parallel , tetapi untuk kasus parallel nilai R_ek lebih kecil , sehingga P_total = V² /R_ek lebih besar.

Perhitungan kita tidak sepenuhnya teliti; bola lampu sungguhan tidak menuruti hukum ohm, dan hambatan bola R = V/I bukan merupakan sebuah konstanta yang tidak tergantung dari selisih potensial V yang melewati bola itu. ( Hambatan filament lampu bertambah seiring dengan suhu pengoperasian yang semakin bertambah ) . tetapi memang benar bahwa bola bola lampu yang dsiambungkan seri yang melalui sebuah sumber akan menyala kurang terang dari pada bila disambungkan parallel melalui sumber yang sama.

c) Dalam kasus seri , arus yang sama mengalir melalui kedua bola . Jika salah satu bola terbakar, maka tidak ada arus sama sekali dala rangkaian itu, dan tidak ada bola menyala. Dalam kasus parallel selsish potensial melalui setiap bola tetap sama dengan 8 V walaupun jika salah satu bola ituhangus terbakar. Maka arus yang melalui bola yang masih berfungsi tetap sama dengan 4 A, dan daya yang diantar ke bola itu tetap sama dengan 32 W, sama seperti sebelum bola lainnya terbakar. Inilah salah satu manfaat susunan parallel dari bola bola lampu. Prinsip ini digunakan dalam sambungan kabel listrik rumah tangga.

Sumber:

1. PPT Dosen

2. http://www.elektronikabersama.web.id/2011/05/bagaimana-menghitung-rangkaian-campuran.html

3. https://djukarna.wordpress.com/2014/09/12/teori-rangkaian-thevenin-norton/

4. http://abi-blog.com/teori-rangkaian-thevenin/

5. http://www.onfisika.com/2013/04/resistor-resistor-dalam-sambungan-seri_15.html